Tweaking the FDV301N Spice model: Cgs

To improve my Spice model of the FDV301N MOSFET I need to understand a little more about how they work. A lot of the dynamic behavior can be modeled as three capacitors: Cgs, Cgd, and Cds. The complexity, as seen in the model provided by Fairchild (diagrammed in the previous post), comes from the fact that the value of Cgd changes as Vgd changes. This post focuses on measuring and modeling the simplest of these: Cgs, the capacitor between the Gate and the Source.

To make life more fun, the data sheet doesn't give the value of Cgs. They give three other values, Ciss, Coss, and Crss:

My research says that Cgs can be calculated as Cgs = Ciss - Crss, so Cgs for the FDV301N should be 8.2pF. The updated Spice model Fairchild provides models Cgs as 8.5pF, which seems close enough. But how do you compare this against the real device?

As a MOSFET is driven on with a constant-current source, its gate voltage does not rise linearly. As the drawing on the right (from ON Semiconductor publication AND9083/D) shows, Vgs behavior can be characterized in three phases. In phase A (red), the gate current is charging Cgs, but Vds has not begun changing. In phase B (blue), the transistor begins to conduct and Vds begins to drop, which means the voltage across Cgd is also changing. With the gate current being consumed charging Cgd, Vgs does not change. In phase C (green), Vds has reached its minimum (or near enough to it) and the gate current goes toward charging both Cgd and Cgs.

Long ago I created an LTspice model of a chain of FDV301N inverters for simulation testing. To this I added 10pF capacitors between the gates and ground to represent my oscilloscope probes. I also replaced the U2 device, which used the Fairchild Spice model, with the X2 device, which is based on my sub-schematic version of this same model.

How can we use this to determine whether the model's Cgs matches that of a real FDV301N? Let's look at the behavior of X1 in our inverter chain. If we pretend that the load resistor of the previous inverter (R1) is a constant-current source, we can calculate the charge and the lumped capacitance of C2 and Cgs of X1. Okay, so a resistor makes a lousy constant-current source, but the first 1V rise of an RC circuit being driven to 5V is a reasonable first approximation.

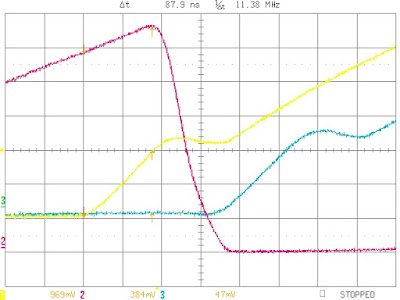
I ran a simulation, probed the S1, S2, and S3 nets, and zoomed into the area where S1 rises, S2 falls, and eventually S3 rises. Here's what it looked like:

It's hard to judge from just the graph, but the time from when S1 begins to rise until S2 begins to fall is about 88ns. This is the phase which represents Cgs charging. If our model is correct, we should see the same behavior on the breadboard:

Well, what a surprise! The simulation matches the model. This suggests that the simulation models Phase A pretty well. What happens after that, in Phase B, is not so good, but that's fodder for another post.

[Edit: I've been asked several times to email the SPICE model I used. It can be downloaded from this link.]

Another attempt at simulation

I really haven't been in the mood to finish any of the PCB layouts, but I didn't want to let this project languish untouched. One of the items on my list has been to get valid simulation results so I can predict whether my choice of pull-up resistors is valid.

In the interim there's been an update to the published Spice model for the FDV301N MOSFET. One of the changes was to change the Cgs value from 78pf to 8.5pf, which makes much more sense to me. I re-ran the simulation from June 2012, and found the new model reduced the per-stage propagation delay from about 200ns to 105ns. This is an improvement, but still longer than the 70ns or so I'm seeing on the breadboard when the effects of the scope probe loading is factored out.

I'm still comparing the simulation results with the actual tracings to understand what needs tweaking to make the simulation more accurate. To make it easier to understand this rather complex model I drew the FDV301N model using the LTspice schematic capture:

The resulting netlist differs from the original model only in comments and minor formatting; otherwise it's identical right down to the net names. I no longer wonder why simulations using this model are so slow.

In the process I think I've discovered an error: the negative output of the EDB voltage source is connected to net 0 (ground), which makes no sense given that the positive output is connected via diode D to the FET's drain pin.  It seems to me that only things related to the temperature input (net 50) should be referenced to ground. I don't think this is affecting the test simulations, since all the Source pins (net 30) are connected to ground, but it would affect some of my real circuits.